
(pour la version anglaise, cliquer sur le drapeau)
Nous construirons un modèle à plusieurs "niveaux synchroniques", en partant de l' hypothèse que notre modèle élémentaire peut
représenter tout niveau d' une organisation quelconque.
Nous parlerons, alors d' "analyse diachronique".
![]()
Modèle à deux niveaux :
Degré de liberté de la commande de A :
Degré de résolution de S au niveau du pilote :
Définition d'une application de A sur S au niveau du pilote:
|
Critère de commandabilité d'un système :
| Critère d'asservissement d'un système : |
Pilotage du niveau 1 par le niveau 2:
Fréquence des transactions :
![]()
Dans le chapitre sur l'analyse synchronique, nous avons passé en revue toute la gamme de transactions qui peuvent lier A et S, depuis l' action unique et parfaite (efficiente) d 'un jeu en univers certain présentant un "col", jusqu' à l' échec de la transaction nécessitant la redéfinition des états de A et S.
Nous avons vu que l' un des moyens de A pour diminuer son niveau d' incertitude consiste à diminuer le nombre d' états de A et S à prendre en compte.
Nous nous proposons de montrer qu' une structure à deux niveaux permet :
De diminuer l' incertitude du niveau supérieur en agrégeant les états de A et S,
D' augmenter l' efficience du niveau inférieur grâce à son pilotage par le niveau supérieur.
Un modèle à deux niveaux est schématisé de la façon suivante :
|
Ce modèle est composé de deux "sénaires" élémentaires superposées, alignées selon un axe orienté qui indique le sens d' intégration du système.
|
|
retour
![]()
Nous formulerons l' hypothèse selon laquelle le pilote suit la même logique que le niveau piloté.
Il cherche en premier à éviter les états indésirables, et souhaite, dans la mesure du possible, gérer l' état de S grâce aux actions de A.
Si l' Acteur a pu définir un élément neutre (voir analyse synchronique), alors tout sous-ensemble d' états de A est stable pour Å.
Toute action étant son propre symétrique, tout sous-ensemble Hi =
(a1,...., ak, e) de décisions prises dans A, exclusives les unes des autres est un sous- groupe de (A, Å).
Nous pouvons donc décomposer (A, Å) en une somme de sous-groupes tels que :
![]()
De la même façon, nous pouvons décomposer S en sous-groupes :
retour
![]()
La volonté de A de contrôler les réactions de S se ramène, au niveau du pilote, à la recherche d' une application de l'ensemble des commandes de A sur un ensemble de sous-groupes de S:
Considérons tout d' abord la fonction F suivante :
S est dit parfaitement commandable, lorsque :
S est asservi à la commande de A si:
Pour la suite du raisonnement, nous prendrons le cas restrictif où S est commandable et asservi, c' est à dire le cas où F est une application :
![]()
Nous pouvons compléter notre modèle de la façon suivante :
|
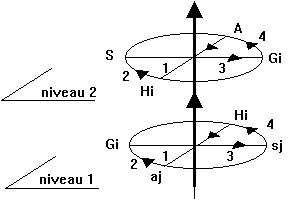 |
L' utilité du pilotage est double :
En limitant les états accessibles par A au premier niveau à Hi, le pilotage améliore l' efficience des actions élémentaires.
De même, en ramenant la description de S à celle de Gj le pilote diminue l' incertitude des niveaux 1&2, en limitant pour chacun d'eux le nombre de situations à envisager (voir stabilité et information)
.
Les actions du Pilote - niveau 1 - sont des actions "stratégiques", tandis que celles du niveau 2, qui restent en quelque sorte des mises en oeuvre des décisions prises au niveau supérieur, sont des actions "tactiques".
Lorsque la réaction de sj de S n' entre pas dans le sous-groupe attendu, la transaction élémentaire n' est plus bouclée et nous sommes devant le cas catastrophique déjà évoqué (voir analyse synchronique).
Il faut, pour terminer la transaction, que le niveau supérieur redéfinisse le jeu, c' est à dire redéfinisse G et H.
retour
![]()
Lorsque les transactions du système piloté se déroulent sans interruption, il n' y a pas de raison de faire appel au pilote.
Dans la mesure où le pilotage a pour fonction d' améliorer l' action du niveau piloté, alors il intervient essentiellement en cas de "catastrophe".
Il s' ensuit que la fréquence des transactions doit diminuer en passant d' un niveau au niveau supérieur.
Le modèle précédent peut être développé et comporter autant d' étages que de besoin.
Dans un tel modèle, nous nous proposons de caractériser chaque niveau synchronique par sa fréquence de transaction, et de définir une loi reliant ces fréquences entre elles.
Nous pouvons maintenant préciser notre problématique de la façon suivante:
En définissant une telle loi, nous voulons caractériser par la mesure d' un écart à celle-ci, certains dysfonctionnements organisationnels dont les théories classiques des organisations ont du mal à rendre compte.
Pour illustrer notre propos, considérons le niveau intermédiaire d' une hiérarchie à 3 niveaux.
Il est assez ordinaire d' observer deux types de dysfonctionnement:
Le niveau intermédiaire n' a pas la compétence requise pour assumer sa tâche de pilotage du niveau inférieur.
Il lui est donc nécessaire d' intervenir fréquemment pour résoudre les crises du niveau inférieur.
Par conséquent, la fréquence de ses transactions aura tendance à s' élever.
Le niveau de pilotage "colle" au niveau inférieur.
A l' inverse, il peut vouloir se rapprocher du niveau supérieur (pour se valoriser, par exemple).
Il aura donc tendance à moins intervenir sur le niveau inférieur : il se "satellise".
Ceci se traduit par une coupure plus ou moins franche du flux d 'informations au passage de ce niveau.
C' est par un phénomène de ce type qu' en général un état major se coupe de sa base opérationnelle.
On peut concevoir qu' une organisation cherche à rendre l' activité de toutes les sénaire à peu près homogène, indépendamment de leur position hiérarchique.
Du fait que la fréquence de transactions est plus faible pour le pilote que pour le système piloté, ceci permet au pilote de gérer plusieurs processus en parallèle.
Une telle organisation conduit à une hiérarchie de type "pyramidale", dans laquelle la population de chaque niveau synchronique est fonction de la variation de fréquences de transactions d'un niveau à l'autre.
retour
![]()
![]()
Nota:
Pour en revenir à notre introduction, notre intention est même plus forte que cela :
le modèle sénaire permet de décrire toute transaction, y compris les liens unissant l'observateur à son objet d'observation, ou bien ceux de ce même observateur face à l'ensemble de ses pairs lorsqu'il explique son expérience ou sa théorie (la présente théorie incluse, bien entendu).
retour
![]()
![]()