Approche thermodynamique des organisations:

Après avoir utilisé le même modèle élémentaire pour conduire nos différentes analyses (synchroniques et diachroniques), nous pouvons considérer celui-ci comme une sorte de "modèle atomique " susceptible de représenter tout type de transaction au sein d' une organisation quelconque.

En associant à chaque action l' énergie qu' elle met en jeu, nous appliquerons à cet atome bien particulier les résultats établis par Boltzmann pour la théorie des gaz parfaits.

Nous proposerons alors de caractériser la performance globale d' une organisation grâce à la mesure des fréquences de transactions propres à chaque niveau hiérarchique.

Jusqu'à présent, nous avions défini les différentes possibilités d'interactions entre dipôles d'une même sénaire sans tenir compte de la plus ou moins grande facilité qu'il y a, pour un Acteur, à concrétiser une décision.
Nous allons maintenant entrer dans le détail de l' économie des transactions en associant à chacune d' elles une dépense d' énergie.

Sommaire

Hypothèses:
Énergie de liaison:
Définition de l'état stable d'un niveau synchronique:
1. Répartition des sénaires
2. Température statistique
Définition des échanges diachroniques:
Le modèle sénaire défini comme "moteur symbolique":
Efficacité et efficience d' une organisation:
Conclusion :

retour vers "home_page"

1/ Hypothèses:

Nous nous situons à un niveau synchronique dans lequel notre système est représenté par un grand nombre de sénaires "semblables".
Afin de conduire nos calculs plus simplement, nous ferons les hypothèses suivantes:

	*Chaque sénaire d'un même niveau est interchangeable:* Nous cherchons avant tout d'éventuelles lois régissant les grands groupes (comme les bureaucraties). Nous nous plaçons ici dans le cas de grandes structures, au sein desquelles il est impossible de diriger un ensemble de personnes par un contact direct et personnalisé. Soit N le nombre de sénaires élémentaires du niveau synchronique considéré .
	*Dans chaque sénaire les actions sont bouclées:* Dans une sénaire, le nombre de classes d'états de chacun des deux dipôles est le même. Chacune est commandable et asservie. Cette hypothèse revient à évacuer tout problème lié à l'efficience des transactions.
	*Les états d'un dipôle sont équiprobables:* C' est une hypothèse "faible" qui maximise notre incertitude quant aux transactions en cours au sein d'une sénaire. Ce faisant nous prenons en compte notre incapacité à connaître en détail chaque sénaire particulière.

retour

2/ Energie de liaison:

Considérons, dans une sénaire, un dipôle A cherchant à agir sur son dipôle complémentaire S.
Dans ces conditions, nous allons supposer qu'aucune action entreprise n'est "gratuite": elle implique la mise en circulation d'une certaine énergie de la part de l' acteur lors d'une transaction.
A chacune des possibilité de transaction, nous associerons une énergie de liaison.
Nous reviendrons ultérieurement sur la possibilité de mesurer cette énergie.
Retenons ici simplement qu'il s'agit d'un quantité mesurable, comme par exemple un coût ou un nombre d'heures.
Notons que cette énergie varie par sauts discrets, lorsque la sénaire passe d'un état à un autre.

	Soit *(s+1)* le nombre d'états énergétiques accessibles à une sénaire (c'est à dire le nombre de configurations de valeurs énergétiques différentes pouvant être prises par cette dernière):
	Soit wi, la valeur de l' état énergétique i avec *i Î (0,..., s)*
	Soit gi; le nombre de transactions d' une sénaire dans l' état énergétique wi,
	Soit ni; le nombre de sénaires dans l' état énergétique wi,
	Soit N, le nombre total de sénaires du niveau synchronique considéré.
	Soit E, l'énergie interne du modèle (au niveau synchronique considéré).

Nous ferons de plus les hypothèses suivantes:

	N l' ensemble des sénaires, à ce niveau synchronique est constant
	E l' énergie de liaison globale (équivalent d'un budget pour un service ou un compte d'heures pour un projet) est constante.

Dans ces conditions, nous avons singulièrement rapproché notre problème de répartition des sénaires constituant un niveau synchronique de celui de la répartition énergétique des molécules dans un gaz parfait.
Ce rapprochement est possible du fait que le modèle sénaire est "global", c'est à dire qu'au niveau synchronique considéré, l' état de chaque sénaire est sans corrélation avec celui de ses voisines de même que dans un gaz, dans les calculs développés par Boltzmann, chaque atome est sans interaction avec ses voisins.
retour

3/ Définition de l'état stable d'un niveau synchronique:

Nous pouvons partir de la remarque suivante: malgré notre incertitude, nous nous occupons de la description d'un système formé, c'est à dire d'un objet doué d'une stabilité suffisante pour pouvoir être observé.
Le problème qui se pose à nous n'est pas de connaître la situation particulière de chaque sénaire prise individuellement, mais de rechercher, pour l'ensemble qu'elles forment, leur répartition la plus probable, qui nous apparaîtra donc la plus stable.
Cette configuration est, par définition même, celle qui pourra être atteinte du plus grand nombre de façons possible.
Notre étude se réduit alors à rechercher un état particulier de notre niveau synchronique pouvant être atteint d'un plus grand nombre de façons que les autres: ce sera l'état stable recherché.

3.1/ Répartition des sénaires à l'état stable d'un niveau synchronique:

Les hypothèses précédentes étant faites, nous pouvons suivre le raisonnement fait par Boltzmann pour la première fois en 1896 pour les gaz parfaits.

Le nombre de modes de répartitions P possible des différentes sénaires sur les niveaux énergétiques qui leurs sont accessibles est:

(voir le paragraphe "Stabilité et Information")

La répartition la plus probable est celle qui pourra être réalisée du plus grand nombre de façons possibles, c'est-à-dire celle pour laquelle P sera maximal.

C' est dire que l' on retrouve formellement les conditions de la thermodynamique statistique.
Avec les hypothèses faites

	N suffisamment grand,
	N= constante,
	E = constante

nous retrouvons les résultats thermodynamiques classiques.
Le nombre d'éléments au niveau énergétique wi a pour expression:

avec

Pour simplifier la suite, nous prendrons le cas particulier où tous les gi sont égaux à 1: chaque transaction possède une énergie de liaison spécifique.

En supposant que le niveau le plus peuplé soit le niveau d'énergie zéro, le nombre de sénaires à cet état est

L'équation précédente devient alors:

.
Les populations ni décroissent très vite lorsque l'on s'éloigne du niveau énergétique fondamental

et la forme même de cette décroissance dépend de la valeur du coefficient b.
Plus sa valeur est grande, plus la décroissance est rapide.

La valeur de b traduit, en termes énergétiques, la plus ou moins grande conformité de comportement des acteurs.

3.2/ Température statistique et fréquence de transactions:

Le produit

est sans dimension (puisqu' il apparaît comme exposant de e ).
Si nous continuons à nous référer à la théorie cinétique des gaz, wi y apparaît comme une énergie de vibrations variant par quantités discrètes sous la forme générale suivante:

où n est une fréquence de vibration caractéristique dépendant du type d'énergie envisagée.

Ce qui nous intéresse dans l'expression quantique précédente, c'est la possibilité de caractériser une énergie par une mesure de fréquence.

Nous garderons l' hypothèse suivante:

Pour un niveau synchronique donné, il est possible d'exprimer l'énergie propre d' une transaction par référence à une fréquence de base.

Considérons maintenant b, c'est une mesure caractéristique de l'ensemble des sénaires du niveau synchronique considéré.

	Nous noterons le b caractéristique du niveau synchronique j:
	Nous définirons alors par nj la "fréquence de contacts caractéristique" du niveau synchronique j considéré, telle que:

Dans ce sens, 1/ nj est bien une mesure de l' "agitation", ou de l' "effervescence" caractéristique d'un niveau synchronique, et nous donnons, par là, un contenu à l'intuition commune selon laquelle un accroissement de liberté d'action s'accompagne d'une augmentation de l'activité et d'une manière générale, des échanges.

retour

4/ Définition des échanges diachroniques:

Considérons maintenant une organisation, définie par m niveaux synchroniques.

Nous envisagerons les échanges entre les sénaires du niveau j avec le niveau inférieur j-1:

Considérons l'ensemble des sénaires d'un même niveau, deux types de fluctuations peuvent se produire:

les niveaux d'énergie peuvent changer de valeur.
les populations des différents niveaux d'énergie peuvent évoluer.

La variation énergétique dE résultant de ses deux types de fluctuation se défini par la relation suivante:

Par définition :

Le premier terme, impliquant une fluctuation de réalisabilité de l'ensemble correspond à un échange de chaleur :
Ce réarrangement des effectifs entre niveaux énergétiques tient au "vécu" de chacune des sénaires formant la population considérée.
En effet, si nous conservons notre optique particulière consistant à dire que le niveau supérieur j+1 défini les règles du jeu régissant la vie du niveau inférieur j d'une organisation, alors, jusqu'à remise en cause du modèle ainsi créé, seuls deux causes peuvent amener les sénaires du niveau j considéré à se répartir différemment:

Leur libre arbitre,
soit dQj la mesure de cette variation,

Les informations recueillies par chaque sénaire à un niveau d'analyse inférieur,
soit dQj-1 cette variation.
Le second terme n'induisant aucune fluctuation de la réalisabilité de l'ensemble correspond à un échange de travail :
Soit d Wj la quantité de travail effectuée au niveau j
(accroissement du rythme des transactions).

Une variation de l'énergie du niveau j s'écrit:

Or nous avons vu qu'une fois défini par le niveau supérieur j+1, notre modèle, tant qu il n'est pas remis en cause, n' évolue plus et n' a pas, par définition d' ouverture sur l' "extérieur", donc :

retour

5/ Le modèle sénaire défini comme "moteur symbolique":

On démontre en thermodynamique que

Nous allons rapprocher l' expression précédente du rapport entre la réalisabilité Pe et un échange de chaleur dQ.
En effet, en prenant en compte que la constante d'intégration b caractérise le niveau synchronique considéré on a :

	d Ln Pj est la variation de réalisabilité du niveau j déterminée par l'exercice du libre arbitre des sénaires à ce niveau.
	d Ln Pj-1 est la variation de réalisabilité du niveau j-1 accompagnant le transfert de avec le niveau supérieur.

Nous faisons l'hypothèse que l'ensemble du modèle, ainsi que chacun des niveau synchronique est à l'équilibre, ce qui implique qu'une variation de réalisabilité à un niveau donné doit être équilibrée globalement par la somme de toutes les variations observables dans les autres niveaux du modèle.
Comme nous ne considérons que deux niveaux synchroniques consécutifs, ceci implique:

D'où :

ou :

Puisque la sénaire prend de la chaleur du niveau inférieur, et qu'elle en créé à son propre niveau, pour qu'un travail soit réellement fourni :

Nous retrouvons ici le théorème connu en thermodynamique sous le nom de théorème de Carnot indiquant qu'une machine thermique ne peut fournir un travail qu' en prenant de la chaleur à une source chaude pour en céder à une source froide.

Ceci permet d'introduire une notion importante, susceptible de servir de mesure de l' efficacité d' une organisation: le rendement thermique.

Le travail recueilli dans les conditions conservatives idéales (ce qui est le cas ici) est au plus:

Soit h le rendement définit par le rapport:

, avec

Considérons maintenant une analyse diachronique s'intéressant à m étages synchroniques.
Optimiser l' échelonnement des fréquences fondamentales de transaction nj revient à optimiser le rendement global n du modèle complet.

Si l'on connaît, par l'expérience, les fréquences de contacts aux niveaux le plus élevé et le plus bas, il est facile d'en déduire l'échelonnement des niveaux intermédiaires: l' optimisation de h implique en effet que tous les rendements soient égaux entre eux.
On peut prendre comme mesure, non pas la fréquence de transactions, mais le temps élémentaire pris par celles-ci, en posant:

retour

6/ Efficacité et efficience d' une organisation:

Nous avons trouvé une relation liant le rendement d'une organisation à la mesure des fréquences de transactions caractérisant les échanges entre dipôles d'une sénaire pour chacun des niveaux d'analyse retenus.
En comprenant la notion de rendement comme précédemment défini, nous énoncerons la règle suivante:
Le modèle sénaire optimum d'un système, pour un nombre de niveaux d'analyse synchronique donné, sera celui pour lequel le rapport des temps de liaisons intra-sénaires de deux niveaux consécutifs quelconque sera une constante.
Prenons pour fixer les idées, une organisation très simple constituée d' un seul service dont les transactions élémentaires sont de l'ordre de 5 mn (fonctionnement d'un guichet, par exemple) et donc les résultats font l' objet de contacts hebdomadaires avec la hiérarchie :
On a :


	pour une journée de 8 h et 5 jours ouvrés par semaine.

alors :

Si nous introduisons maintenant un niveau de maîtrise, intervenant toutes les 2 heures on a alors:

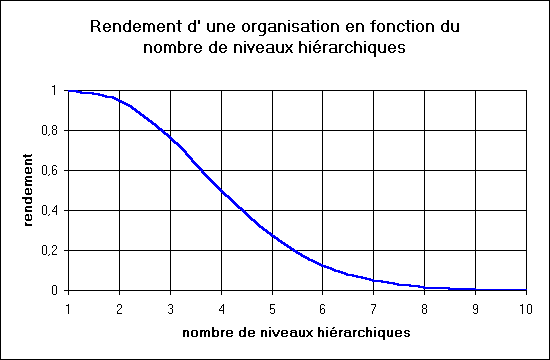
En augmentant le nombre de niveaux hiérarchiques, pour rendre plus souple, plus adaptable une organisation, nous diminuons son rendement.

Nous voyons donc que :

pour accroître l' efficacité d' une organisation, il faut diminuer le nombre de niveaux hiérarchiques (c' est en particulier le "down sizing" très en vogue actuellement),
pour améliorer son efficience, il faut complexifier sa structure (c' est en particulier une conséquence de la recherche de la qualité).
Il appartient à l' organisateur d' optimiser le nombre de niveaux en fonction du but qu' il assigne à l' organisation. Il n'y a donc pas de "meilleur" modèle qui puisse être défini indépendamment des buts de l' organisateur.
retour

7/ Conclusion :

Pourquoi tenter de formaliser un domaine qui reste le lieu privilégié de la praxis ?
La réponse que je serais tenté de fournir se situe à deux niveaux:

Concernant le champ d' application proprement dit :

La description des processus organisationnels à l' aide de modèles sénaires est assez simple et s' offre au modélisateur comme moyen de communication.
Son utilité pourrait être comparée à celle du langage GRAFCET pour les processus industriels.

Une modélisation standardisée permet des études comparatives entre organisations ou groupes d' organisations hors de toute référence aux flux monétaires. Ceci permet d' élargir la notion de compétitivité au delà du domaine marchand.

D' autres questions peuvent alors être abordées, d' autres dysfonctionnements mis en évidence :

	Quel sont l' *efficacité* et l' *efficience* d' un état major ?
	Quelle structure adopter en fonction de celle de son adversaire ?
	Quel est le rendement d'une entreprise ?

Concernant la théorie elle-même :

	Les passerelles que nous avons esquissées entre notre modèle sénaire et des théories plus établies telles que la théorie des jeux, la théorie de l' information, et la thermodynamique sont un facteur d' ouverture. Grâce à cette formalisation, il devient possible d' asseoir l' étude des organisations, sur la mesure de phénomènes physiques.
	Par ailleurs, des voies nouvelles s' offrent alors à nous. Il serait par exemple intéressant de regarder la stratification d' une organisation en différents niveaux synchroniques comme une représentation par des "groupes de renormalisation". Le point à étudier serait alors la définition du "*point critique*" d' une organisation.
	Une autre voie serait peut être de considérer notre modèle comme une fractale. La "*dimension fractale*" caractéristique d' une organisation serait alors le temps.

retour

retour vers "home_page"

note 1 :

Une sénaire n' est pas assimilable à une entité physique, telle un individu ou un service, car ce modèle ne représente que des processus interactifs entre entités.
Le travail d' un individu particulier au sein d' une organisation peut être décrit par un ensemble de sénaires, s' inscrivant sur les niveaux hiérarchiques différents.

retour

note 2 :

Pour N suffisamment grand, on utilise plus commodément la "réalisabilité" de P, définie par son logarithme :

Pour que P soit maximum, il faut que la différentielle soit nulle :

On intègre les deux condition sur N et E en écrivant : et

En ajouter membre à membre les deux conditions précédentes affectés de coefficients arbitraires a et b on a :

Cette expression doit être satisfaite quelque soit dni, ce qui donne le nombre ni d'éléments se trouvant au niveau wi à l'état d'équilibre, c'est-à-dire lorsque Pe est maximum:

retour

note 3 :

Cette hypothèse ne nuit pas à la généralité du raisonnement.

retour

note 4 :

On peut démontrer que dans le cas où le niveau k le plus peuplé a une énergie wk différente de 0, la relation précédente prend deux expressions, suivant que l'on considère les populations des niveaux supérieurs ou inférieurs à wk.

	Niveaux supérieurs:
	Niveaux inférieurs:

retour

note 5 :

Pour des raisons pratiques, on utilise en thermodynamique la notion de température absolue, nombre sans dimensions égal à l' inverse de la température statistique multiplié par une constante ayant les dimensions d' une énergie. : .

Nous préférons introduire ici la notion de " fréquence de transactions", plus directement adaptée à notre sujet. Mais, les notions de fréquence et de température sont liées: T est bien une mesure de " l' agitation thermique" moyenne d' un gaz.

retour

note 6 :

Supposons possible de construire un modèle présentant un nombre de niveaux infini, chacun d'eux reprenant le même motif élémentaire, les différents niveaux ne différent les uns des autres que par la valeur de b.

A l'optimum, tel qu'ici définit, chaque niveau se déduit du précédent par une homothétie de rapport ou

Ceci revient à faire d'un tel modèle un objet dont le temps est une dimension fractale.

retour

note 7 :
Remarquons que cet étagement est proche de l'optimum : en effet 1/24 est peu différent de 1/20. Par exemple, si l'on considère un système dont les niveaux extrêmes ont des temps de transaction de 5 mn, pour le plus bas et d'une année au niveau le plus élevé; le rendement varie de la façon suivante, en fonction du nombre de niveaux intermédiaires:

retour

retour vers "home_page"

	Leur libre arbitre, soit dQj* la mesure de cette variation,*
	Les informations recueillies par chaque sénaire à un niveau d'analyse inférieur, soit dQj-1* cette variation.*

	pour accroître l' efficacité d' une organisation, il faut diminuer le nombre de niveaux hiérarchiques (c' est en particulier le "down sizing" très en vogue actuellement),
	pour améliorer son efficience, il faut complexifier sa structure (c' est en particulier une conséquence de la recherche de la qualité).